Лимитите на креативността: Няколко интересни парадокса, които надхвърлят логиката

Парадоксът е твърдение или проблем, който или изглежда води до два напълно противоречиви (но възможни) резултата, или предоставя солидни доказателства за твърдение, което противоречи на интуитивното ни очакване.

Това изречение е грешно.

Парадоксите са централна част от философското мислене от векове и не пропускат да ни предизвикат, преобръщайки нашата представа за истина, като ни представят доказуемо правдоподобни ситуации, които всъщност са също толкова доказуемо невъзможни.

Та това ще направим сега – ще разгледаме няколко любопитни ситуации, които ще ни покажат колко неочакван може да бъде света.

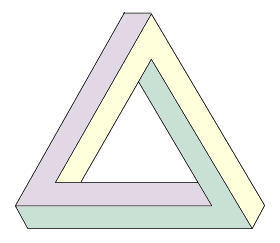
Триъгълникът на Пенроуз

Докато повечето парадокси са представени чрез думи, някои са визуални – например, триъгълникът на Пенроуз. Това е обект, който е описан от един от неговите създатели като „невъзможност в най-чистата й форма“. С две думи – става въпрос за двуизмерна манипулация с пропорциите на триизмерен триъгълник.

Първоначално фигурата е изобразена от шведския художник Оскар Ройтерсверд през 1934 г. Но 24 години по-късно – когато британския математик Роджър Пенроуз и баща му публикуват статия за нея – тя добива значителна популярност.

След това, не толкова самият триъгълник, колкото принципът на парадоксалността му може да се забележи в творбите на Мориц Корнелис Ешер; особено във „Водопад“.

Парадоксът на Хилберт за хотелските стаи

Този парадокс представлява мисловен експеримент, който има за цел да покаже объркващата природа на безкрайността.

Представете си, че влизате в голям хотел и си търсите стая. Колко голям? Безкрайно голям – с изброимо безкраен брой стаи. Но в момента всички те са заети от изброимо безкраен брой гости. (Изброимо безкрайно означава, че можете едно към едно да прикрепите естествено число към всяка стая, тоест да й дадете пореден номер.) Може да се предположи, че хотелът няма да може да ви настани, да не говорим за още гости… но парадоксът на Хилберт доказва, че това предположение е безкрайно грешно.

За да ви настани, хотелът може хипотетично да премести госта от стая 1 в стая 2, госта от стая 2 в стая 3, госта от стая 3 в стая 4… тоест, всеки гост от текущата му стая x, в нова стая x+1. Тъй като има безкрайно много стаи, всеки ще получи нова и същевременно стая 1 вече ще е напълно празна за вас. Приятен престой.

Но какво ще стане, ако искаме да приложим тази идея към произволен ограничен брой гости? Да кажем, че 3000 души пристигат и искат стаи. Ами няма проблем – повтаряме упражнението, но вместо x+1, просто правим x+y, като y в този случай е 3000.

И сега ултиматният въпрос – какво става ако се наредят изброимо безкраен брой нови гости, всеки от които иска стая във вече заетия от изброимо безкраен брой гости хотел с изброимо безкраен брой стаи? Има решение и за този случай: просто моделът сега ще бъде 2x: преместваме госта от стая 1 в стая 2, госта от стая 2 в стая 4, госта от стая 3 в стая 6 и т.н. Това ще остави свободни всички стаи с нечетни номера, така че всеки нов гост ще може да заеме една от тях, а всички предишни посетители ще бъдат преместени в следващата четна стая.

Готиното на този парадокс е, че предлага безспорно доказателство за контраинтуитивно твърдение. А именно че в един хотел с безброй много заети стаи можем да настаним още безброй много нови гости…

Главен отговорник за парадокса е философът Дейвид Хилбърт, който го излага за първи път в лекция от 1924 г. и оттогава се използва за демонстриране на различни принципи на безкрайността.

Годфри Харолд Харди

Парадоксът на интересното число

Това вероятно изобщо не е парадокс, въпреки че често се нарича така. По същество той доказва, че всички числа са „интересни“ – дори скучните, защото те всъщност са интересни именно с това, че са скучни…

Интересно в този случай означава, че числото има нещо уникално за себе си. Например 1 е първото ненулево естествено число; 2 е най-малкото просто число; 3 е първото нечетно просто число. Списъкът може да продължи безкрайно, докато стигнете до първото „безинтересно“ число. В него няма нищо специално или вълнуващо. Но тъй като е първото безинтересен число, на който сте се натъкнали, то всъщност е уникално с това – и следователно интересно.

И този процес може да продължи безкрайно…

Тази идея се роди в резултат на дискусия между математиците Сриниваса Рамануджан и Г. Х. Харди. Харди отбеляза, че номерът на таксито, в което се е возил наскоро, 1729, е „доста скучен“. Рамануджан отговаря, че всъщност е интересен, тъй като това е най-малкото число, което е сумата от два куба по два различни начина:

1729 е сумата от кубовете на 10 и 9. 10³ = 1000, а 9³ = 729. Съответно сборът на двата куба е 1729.

И вторият начин – кубовете на 12 и 1. 12³ = 1728, а 1³ = 1. Заедно те отново правят 1729.